Aritmética y Álgebra: Explorando los Fundamentos de las Matemáticas

La aritmética es la rama de las matemáticas que se encarga del estudio de los números y las operaciones que se realizan con ellos: suma, resta, multiplicación y división. El término proviene del griego aritmetikos, compuesto por la raíz arithmos (números) y el sufijo –tikos (ciencia): ciencia de los números.

Se conoce como álgebra a la rama de la matemática en la cual las operaciones son generalizadas empleando números, letras y signos que representan simbólicamente un número u otra entidad matemática.

Historia y Figuras Clave

Diofanto de Alejandría es considerado el padre del álgebra, quien recogió la tradición egipcia y babilónica, ampliándola y mejorándola en su libro “Las Aritméticas”. Sus principales trabajos incluyen el análisis diofántico y la obra de Las Aritméticas.

La palabra álgebra proviene del título de un libro, Al-jabr w’al-muqabalah, escrito alrededor del año 825 por el matemático y astrónomo Mohammed ibn- Musa al-Khwarizmi, que muestra en sus trabajos la primera fórmula general para la resolución de ecuaciones de primer y segundo grado.

Arquímedes se basó en las matemáticas para sus tratados de física y geometría del espacio.

Herón también se basó en ellas para hacer algunos de sus inventos, como la primera máquina de vapor.

Mujeres en las Matemáticas

Teano: Primera mujer matemática. Fue discípula de Pitágoras y se casó con él. Enseñó en la escuela pitagórica.

Hipatia de Alejandría: Contribuyó a la invención de aparatos como el aerómetro y construyó el astrolabio. Trabajó sobre escritos relacionados con las ecuaciones diofánticas, sobre las cónicas y la geometría, y también elaboró tablas sobre movimientos de los astros. En el año 415, cuando tenía 45 años, fue asesinada por monjes fanáticos de la iglesia de San Cirilo de Jerusalén, ya que ella era partidaria del racionalismo científico griego y no quiso convertirse al cristianismo.

Maria Gaetana Agnesi: Se dedicó en profundidad al estudio del álgebra y la geometría, y nueve años más tarde aparecieron publicadas las Instituzioni Analitiche.

Leyes de los Exponentes

LEY 1: Potencia cero. Cualquier base que se eleva a la potencia 0, el resultado es 1, es decir, equivale al número 1.

LEY 2: Exponente igual a 1. Cuando el exponente es 1, el resultado será el mismo valor de la base.

LEY 3: 1 elevado a una potencia. Cuando 1 es elevado a cualquier potencia, el resultado siempre será 1.

LEY 4: Multiplicación de términos con la misma base, cada uno con su respectivo exponente. Cuando se multiplican una misma base con exponentes iguales o diferentes, su resultado es la misma base elevada a una potencia igual a la suma de las potencias de los factores.

LEY 5: Potencia negativa. Cualquier número real, elevado a un exponente negativo, puede convertirse en una potencia positiva pasándolo al lado contrario de la fracción.

LEY 6: Potencia elevada a otra potencia (potencia de potencia). Cuando una potencia de una base se eleva a otra potencia, el resultado es un término de la misma base con un exponente que es igual al producto de las dos potencias.

LEY 7: Producto elevado a una potencia. Cuando el producto (multiplicación) de dos o más factores se eleva, todo a la vez, a una potencia; el resultado es el mismo producto pero con cada factor elevado a la potencia dada; y viceversa.

LEY 8: División de bases iguales. Cuando se dividen dos potencias de la misma base, su cociente es la misma base elevada a una potencia igual a la diferencia entre la potencia del dividendo y la del divisor.

LEY 9: Cociente elevado a una potencia. Cuando un cociente (división) se eleva, todo a la vez, a una potencia, el resultado es el mismo cociente pero con el dividendo y el divisor elevados a la potencia dada.

Conjuntos Numéricos

• ∩ Intersección
• U Unión
• Aᶜ Complemento

• N NATURALES: Con ellos contamos. Son enteros y positivos (1, 2, 3, 4, …).
• Z ENTEROS: Son todos los naturales y sus opuestos, además del cero (0, 1, -1, 2, -2, 3, -3, …..)
• Q RACIONALES: Los que podemos escribirlos como cociente de dos enteros con tal de que el denominador sea diferente de cero. Los quebrados o fracciones.
• I o Q’ IRRACIONALES: Son números cuya parte decimal tiene infinitas cifras no periódicas 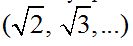No hay ningún número que multiplicado por sí mismo da 2, ni 3, ni 5, ni 7….
• R REALES: Son números que existen. Se llaman números reales a todos los racionales e irracionales.
• i IMAGINARIOS: Como hemos hecho referencia a los números REALES querrá decir que también hay IMAGINARIOS. Es cierto, son aquellos que pueden surgir cuando realizamos algunas operaciones cuyo resultado nos puede dar una raíz cuadrada de un número negativo: 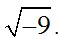No existe ningún número que multiplicado por sí mismo (hemos de incluir su signo) nos dé –9, porque –3 x –3 siempre será 9 y NO –9. Luego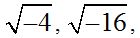 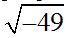son imaginarios.
• c COMPLEJOS: Son números que constan de dos clases de números: reales e imaginarios