Aplicaciones de Matrices
Ejercicio 2
Tres personas, A, B, C, quieren comprar las siguientes cantidades de fruta:
- A: 2 kg de peras, 1 kg de manzanas y 6 kg de naranjas.
- B: 2 kg de peras, 2 kg de manzanas y 4 kg de naranjas.
- C: 1 kg de peras, 2 kg de manzanas y 3 kg de naranjas.
En el pueblo en el que viven hay dos fruterías, f1 y f2:
- En f1 las peras están a 1.5 €/kg, manzanas a 1 €/kg y naranjas a 2 €/kg.
- En f2: peras a 1.8 €/kg, manzanas a 0.8 €/kg y naranjas a 2 €/kg.
a) Expresa matricialmente la cantidad de fruta (peras, manzanas y naranjas) que quiere comprar cada persona (A, B, C).
b) Escribe una matriz con los precios de cada tipo de fruta en cada una de las dos fruterías.
c) Obtén una matriz, a partir de las dos anteriores, en la que quede reflejado lo que se gastaría cada persona haciendo su compra en cada una de las dos fruterías.
Solución:
c) El producto de las dos matrices anteriores nos da la matriz que buscamos:
Ejercicio 3
Tres familias, A, B y C, van a ir de vacaciones a una ciudad en la que hay tres hoteles.
a) Escribe en forma de matriz el número de habitaciones (dobles o sencillas) que necesita cada una de las tres familias.
b) Expresa matricialmente el precio de cada tipo de habitación en cada uno de los tres hoteles.
c) Obtén, a partir de las dos matrices anteriores, una matriz en la que se refleje el gasto diario que tendría cada una de las tres familias en cada uno de los tres hoteles.
Solución:
c) El producto de las dos matrices anteriores nos da la matriz que buscamos:
Ejercicio 4
Una empresa tiene tres factorías, F1, F2, F3, en las que se fabrican diariamente tres tipos diferentes de productos, A, B y C, como se indica a continuación:
- F1: 200 unidades de A, 40 de B y 30 de C.
- F2: 20 unidades de A, 100 de B y 200 de C.
- F3: 80 unidades de A, 50 de B y 40 de C.
Cada unidad de A que se vende proporciona un beneficio de 5 euros; por cada unidad de B, se obtienen 20 euros de beneficio; y por cada una de C, 30 euros.
Sabiendo que la empresa vende toda la producción diaria, obtén matricialmente el beneficio diario obtenido con cada una de las tres factorías.
Solución:
Ejercicio 5
En una pastelería elaboran tres tipos de postres: A, B y C, utilizando leche, huevos y azúcar (entre otros ingredientes) en las cantidades que se indican:
- A: 3/4 de litro de leche, 100 g de azúcar y 4 huevos.
- B: 3/4 de litro de leche, 112 g de azúcar y 7 huevos.
- C: 1 litro de leche y 200 g de azúcar.
El precio al que se compran cada uno de los tres ingredientes es de 0,6 euros el litro de leche, 1 euro el kg de azúcar, y 1,2 euros la docena de huevos.
Obtén matricialmente el gasto que supone cada uno de estos tres postres (teniendo en cuenta solamente los tres ingredientes indicados).
Solución:
Por tanto, el postre A supone 0,95 euros, el B 1,26 euros; y el C, 0,8 euros.
Ejercicio 5
Halla la matriz X2 + Y2, donde X e Y son dos matrices cuadradas de orden dos, verificando:

Solución:



Por tanto:



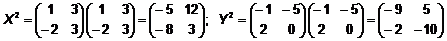

Ejercicio 7
Expresa en forma matricial y resuelve, utilizando la matriz inversa:

Solución:
Obtenemos X:
Por tanto, la solución del sistema es: x = 3, y = 1, z = 0
Ejercicio 8
Maximiza la función z = 3x + 2y, sujeta a estas restricciones:

Solución:

y hallamos la región que cumple las condiciones del problema.
· Representamos la dirección de las rectas z = 3x + 2y, dibujando la que pasa por el origen de coordenadas: 3x + 2y = 0.

· El máximo se alcanza en el punto (100, 50) y vale z = 3 × 100 + 2 × 50 = 400.
Ejercicio 25





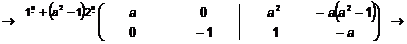

Ejercicio 26
Expresa y resuelve el siguiente sistema de forma matricial:






Ejercicio 27
Se considera la función z = 3x + 2y. Determina el punto donde la función toma su valor mínimo, con las siguientes restricciones:

Solución:

y hallamos la región que cumple las condiciones del problema.
· Representamos la dirección de las rectas z = 3x + 2y, dibujando la que pasa por el origen de coordenadas: 3x + 2y = 0.



Ejercicio 28
Se dispone de 600 g de un determinado fármaco para elaborar pastillas grandes y pequeñas. Las grandes pesan 40 g y las pequeñas 30 g. Se necesitan, al menos, tres pastillas grandes y, al menos, el doble de pequeñas que de grandes.
Cada pastilla grande proporciona un beneficio de 0,2 euros y la pequeña, de 0,1 euros.
¿Cuántas pastillas se han de elaborar de cada clase para que el beneficio sea máximo?
Solución:

Las restricciones son:

La función que nos da el beneficio es z = 0,2x + 0,1y = 0,1(2x + y). Debemos maximizar esta función, sujeta a las restricciones anteriores.
Dibujamos el recinto correspondiente a las restricciones y la recta 0,1(2x + y) = 0
2x + y = 0, que nos da la dirección de las rectas z = 0,1(2x + y).


en (6, 12).
Por tanto, han de elaborarse 6 pastillas grandes y 12 pequeñas. En este caso, el beneficio sería de z = 0,1(2 × 6 + 12) = 2,4 euros.
Ejercicio 43

Solución:



Ejercicio 44
Halla una matriz, X, tal que AX = B, siendo:





