Leyes de los Signos y Exponentes

Ley de Signos

• Suma: El signo del resultado será el del número con mayor valor absoluto.
• Resta: El signo que está en medio se cambia a suma si es de resta, y a resta si es de suma. El segundo signo se modifica.
• Multiplicación:
• División:

Exponentes y Potencias

Los elementos que integran una potencia son:

• Base: El número que se multiplica por sí mismo.
• Exponente: El número que indica cuántas veces se multiplica la base.

Para resolver una potencia, se multiplica la base tantas veces como indica el exponente. Ejemplo: 2³ = 2 * 2 * 2 = 8

Propiedades de las Potencias

• Producto de potencias de la misma base: El producto de potencias de la misma base es igual a la misma base elevada a la suma de los exponentes. Ejemplo: 2³ * 2² = 2⁽³⁺²⁾ = 2⁵
• Potencia de una potencia: La potencia de otra potencia es igual a la misma base elevada al producto de los exponentes. Ejemplo: (2³)² = 2^(3*2) = 2⁶
• Cociente de potencias: El cociente de potencias de la misma base es igual a la misma base elevada a la resta del exponente del dividendo menos el exponente del divisor. Ejemplo: 2⁵ / 2² = 2^(5-2) = 2³
• Potencias con exponente negativo: Todo número con exponente negativo es igual a una fracción, donde el numerador es la unidad y el denominador es el mismo número con exponente positivo. Ejemplo: 2^-3 = 1/2³

Geometría Básica

Construcción de Ángulos y Cuadriláteros

Triángulos

La suma de los ángulos internos de un triángulo es de 180°. Se representa con el símbolo Δ.

Cuadrados

Los cuadrados son cuadriláteros con cuatro lados iguales y cuatro ángulos rectos (90°). La suma de sus ángulos internos es de 360°.

Rectángulos

Los rectángulos son cuadriláteros con cuatro ángulos rectos (90°) y lados opuestos iguales. La suma de sus ángulos internos es de 360°.

Ángulos

Un ángulo es la parte de un plano comprendida entre dos semirectas que tienen el mismo punto de origen o vértice. Se suelen medir en unidades como el grado sexagesimal (°).

Pueden estar definidos sobre superficies planas o curvas. Se denomina ángulo diedro al espacio comprendido entre dos semiplanos cuyos orígenes comunes son una recta.

Amplitud de Ángulos

Se llama amplitud de un ángulo a la medida de este.

Formas Geométricas

Se llama ángulo a la amplitud entre dos líneas de cualquier tipo que se cruzan en un punto.

Región Angular

Se denomina región angular a cada una de las partes en que puede dividir el plano un ángulo.

Forma Trigonometrica

Es la amplitud de rotación en torno a uno de sus extremos.

Ángulos que se Forman entre Paralelas por un Transversal

Cuando una recta transversal corta a dos rectas paralelas, se forman diferentes tipos de ángulos:

• Ángulos opuestos por el vértice: Dos ángulos opuestos por el vértice son iguales. Ejemplo:
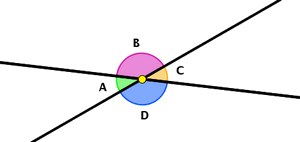
• Ángulos adyacentes: Dos ángulos que tienen el mismo vértice situado entre ellos son adyacentes. Ejemplo:
• Ángulos complementarios: Dos ángulos cuya suma es de 90° y parten del mismo vértice. Ejemplo:
• Ángulos suplementarios: Dos ángulos cuya suma es de 180° y ambos parten del mismo vértice. Ejemplo:
• Nota: Algunos ángulos adyacentes también pueden ser suplementarios.

Ángulos que se Forman entre 2 Rectas Cortadas por una Transversal

• Ángulos opuestos: Dos ángulos opuestos siempre miden lo mismo y son iguales. Ejemplo:
• Ángulos correspondientes: Dos ángulos correspondientes son iguales, es decir, miden lo mismo. Los ángulos correspondientes se localizan en el mismo lado de la transversal, pero en distinta paralela. Ejemplo:
• Ángulos alternos: Este tipo de ángulos se divide en ángulos alternos internos y alternos externos.
  • Ángulos alternos internos: Dos ángulos internos alternos siempre miden lo mismo. Sus características son:
    • Se encuentran dentro de las paralelas.
    • Se encuentran en distintas paralelas.
    • Se localizan del lado contrario de la transversal.
    • Su medida es igual.
  • Ángulos alternos externos: Dos ángulos alternos externos son iguales. Sus características son:
    • Se localizan fuera de las paralelas.
    • Se encuentran en distinto lado de la transversal.
    • Su medida es igual.
    • Se encuentran en distinta paralela.
• Ángulos colaterales: Este tipo de ángulos se divide en dos:
  • Colaterales internos: Para localizar este tipo de ángulos, se necesitan las siguientes características:
    • Se localizan en distinta paralela.
    • Se localizan dentro de las paralelas.
    • Se localizan del mismo lado de la transversal.
  • Colaterales externos: Este tipo de ángulos tiene características semejantes a la anterior, la única diferencia es que los ángulos se localizan fuera de las paralelas. Ejemplo:

Perímetro, Área y Volumen de Algunos Cuerpos Geométricos

Perímetro

El perímetro es la suma de las longitudes de los lados de una figura.

Unidad de Medida

Para el perímetro total, las unidades de medida son las mismas que las de la figura y serán lineales. Ejemplo:

• Si la figura tiene unidades, su perímetro será igual a unidades lineales: Lado = U, P = U
• Si la figura tiene centímetros, su perímetro será igual a centímetros: Lado = CM, P = CM
• Si la figura tiene decímetros, su perímetro será igual a decímetros: Lado = DM, P = DM
• Si la figura tiene metros, su perímetro será igual a metros: Lado = M, P = M, etc.

La fórmula para calcular el perímetro de algunas figuras es a través de la suma de cada uno de sus lados. Ejemplo:

Nota: El círculo es la única figura que no se calcula sumando sus lados, sino que tiene una fórmula específica.

Área

El área es la superficie que se encuentra dentro de una figura geométrica.

Unidad de Medida

La unidad de medida del área se obtiene al elevar al cuadrado la unidad de medida de la figura.

Cuerpos Geométricos

Volumen

El volumen es la magnitud definida como la cantidad de espacio tridimensional que ocupa un cuerpo.

Los cuerpos geométricos limitados por superficies planas se llaman poliedros.

Los cuerpos geométricos están compuestos por vértices, aristas y caras.

Tipos de Cuerpos Geométricos

• Cubo: Es el poliedro que tiene sus aristas iguales y tiene la forma cuadrada. El cubo también es conocido como hexaedro regular. Ejemplo:

El cubo o hexaedro tiene:

• 6 caras cuadradas
• 12 aristas iguales
• 8 vértices