Raíz Cuadrada

La raíz cuadrada es la operación inversa a elevar al cuadrado. Resolver la raíz cuadrada de un número A consiste en encontrar otro número B tal que B² = A. Es decir, consiste en encontrar cuál es el número que multiplicado dos veces por sí mismo da el valor de A.

Propiedades

• La raíz cuadrada de un número al cuadrado es ese mismo número: . Esto es así porque a · a = a²
• La raíz cuadrada de un producto de dos o más números es igual al producto de las raíces cuadradas de cada uno de los factores:
  Ejemplo: queremos calcular la raíz cuadrada de , que podemos expresarla también como . Y podemos resolverla de la siguiente manera:
• El cuadrado de la raíz cuadrada de un número es ese mismo número . Lo podemos afirmar porque
• Ejemplo:
• La raíz cuadrada del cociente de dos números es igual al cociente de las raíces cuadradas de cada uno de los números:
  
  Ejemplo: la raiz cuadra de se puede resolver asi: Pero también podemos hacerlo de la siguiente manera:
  
• Es importante observar que esta igualdad también se cumple en sentido contrario, es decir:
  Ejemplo:
  

Ejemplos

• Ejemplo 1: queremos simplificar y .
  Aplicando las propiedades anteriores, podemos escribir:
  
  
• Ejemplo 2: queremos simplificar la expresión .
  Factorizamos los radicandos, y obtenemos:
  
  Aplicamos propiedades:
  
  Resolvemos cuadrados perfectos:
  
  Sacamos a como factor común:
  
  Por tanto, resolviendo paréntesis, tenemos:
  
  El resultado sería 0.

Racionalización

– Si en el denominador lo único que aparece es una raíz, multiplicamos convenientemente el numerador y el denominador por una raíz de tal forma que se vaya del denominador de la raíz.

– Si en el denominador aparecen dos raíces sumándose o restándose, multiplicamos el numerador y el denominador por el conjugado del denominador .

Ecuaciones Cuadráticas

Es de la forma ax² + bx + c = 0 , donde a, b y c son constantes reales y a ¹ 0.

Resolución de E. Cuadráticas

– Por factorización: resolver la ecuación    x² – 12x – 28 = 0

Factorizamos en trinomio recordando el producto de binomios con un término común, es decir, buscando dos números cuyo producto sea -28 y cuya suma sea -12; estos números son -14 y 2, y la factorización es: (x – 14)(x + 2) = 0

Por lo tanto las soluciones son: X₁ = 14 y X₂ = -2

– Utilizando la fórmula de resolución:

 Para resolver la ecuación cuadrática ax² + bx + c = 0 ,

podemos utilizar la fórmula:

Propiedades de las Raíces

Dada la ecuación de segundo grado ax² +  bx +  c = 0,y x₁ y x₂ sus soluciones, se cumple: 

1. La suma de las dos soluciones o raíces de una ecuación de segundo grado,  x₁ + x₂,  es

2. El producto de las dos soluciones de una ecuación de segundo grado,  x₁ × x₂, es

Ejercicio:

1. Determinar, sin resolver las ecuaciones, el valor de la suma y del producto de sus soluciones:

_Resolución:

a) 2x² + 7x – 15 = 0;  a = 2;  b = 7;  c = -15

_{FUNCION CUADRATICA: es aquella que puede escribe  como una acuacion de la forma:}

 _{f(x) = ax² + bx + c}

donde a, b y c (llamados términos) son números reales cualesquiera y a es distinto de cero (puede ser mayor o menor que cero, pero no igual que cero). El valor de b y de c sí puede ser cero.

En la ecuación cuadrática cada uno de sus términos tiene un nombre.

Así,

ax²  es el término cuadrático

bx es el término lineal

c es el término independiente

Orientación o concavidad

Una primera característica es la orientación o concavidad de la parábola. Hablamos de parábola cóncava si sus ramas o brazos se orientan hacia arriba y hablamos de parábola convexa si sus ramas o brazos se orientan hacia abajo.

Esta distinta orientación está definida por el valor (el signo) que tenga el término cuadrático (la ax²):

Si  a > 0 (positivo) la parábola es cóncava o con puntas hacia arriba, como en f(x) = 2x² − 3x − 5

Si  a ² + 2x + 3

Eje de simetría o simetría

Otra característica o elemento de la parábola es su eje de simetría.

El eje de simetría de una parábola es una recta vertical que divide simétricamente a la curva; es decir, intuitivamente la separa en dos partes congruentes. Se puede imaginar como un espejo que refleja la mitad de la parábola.

Su ecuación está dada por:

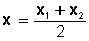
Donde  x₁  y  x₂  son las raíces de la ecuación de segundo grado en x, asociada a la parábola.

De aquí podemos establecer la ecuación del eje de simetría de la parábola:

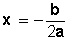
Vértice

el vértice de la parábola es el punto de corte (o punto de intersección) del eje de simetría con la parábola y tiene como coordenadas

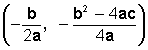
La abscisa de este punto corresponde al valor del eje de simetría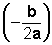 y la ordenada corresponde al valor máximo o mínimo de la función, 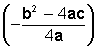según sea la orientación de la parábola (recuerde el discriminante)